>	with(linalg):

 

The code consists of two main programs - symm  and   matrices  and two auxiliary  functions - simple  and   l_f.
The program  symm  is  the main function.
The input consists of a complex-valued polynomial   f(p)  considered as the
projective form of homogeneous binary polynomial F(x,y), and
the degree n=deg(F).   The program computes the invariants J  and  K  in reduced form, determines the dimension of the symmetry group, and, in the case of a finite symmetry group, applies the
Maple command  solve  to solve the two polynomial symmetry equations  (3,4) to find
explicit form of symmetries.  

The output of  symm  consists of the projective index of the form and the explicit formulae for its
discrete   projective symmetries.  The program also notifies the user if the
symmetry group is not discrete,  or is in the maximal discrete symmetry class.  

>

symm:=proc(form,n) global tr,err; local Q,Qp,Qpp,Qppp,Qpppp,H,T,V,U,J,K,j,k, Eq1,Eq2,i,eqtr,ans; tr:='tr': Q:=form(p); Qp:=diff(Q,p); Qpp:=diff(Qp,p); Qppp:=diff(Qpp,p); Qpppp:=diff(Qppp,p); H:=n*(n-1)*(Q*Qpp-(n-1)/n*Qp^2); if H=0 then  ans:=`Hessian is zero: two-dimensional symmetry group` else  T:=-n^2*(n-1)*(Q^2*Qppp-3*(n-2)/n*Q*Qp*Qpp+2*(n-1)*(n-2)/n^2      *Qp^3); V:=Q^3*Qpppp-4*(n-3)/n*Q^2*Qp*Qppp+6*(n-2)*(n-3)/n^2*Q*Qp^2  *Qpp-3*(n-1)*(n-2)*(n-3)/n^3*Qp^4; U:=n^3*(n-1)*V-3*(n-2)/(n-1)*H^2; J:=simple(T^2/H^3);K:=simple(U/H^2); j:=subs(p=P,J);k:=subs(p=P,K); Eq1:=simplify(numer(J)*denom(j)-numer(j)*denom(J)); Eq2:=simplify(numer(K)*denom(k)-numer(k)*denom(K)); if Eq1=0 then   ans:=`Form has a one-dimensional symmetry group`; else   if Eq2=0  then    print (` Form has the maximal possible discrete symmetry              group`); eqtr:= [solve(Eq1,P)];        tr:=map(radsimp,map(allvalues,eqtr));     else        eqtr:=[solve({Eq1,Eq2},P)];        tr:= [];        for i from 1 to nops(eqtr) do         tr:=map(radsimp,[op(tr),allvalues(rhs(eqtr[i][1]))]);        od      fi;    print(`The number of the projective symmetries`=nops(tr));    ans:=map(l_f,tr);    if err=1 then     print(`ERROR: Some of the transformations are not     linear-fractional`)    else     if err=2 then      print(`WARNING: Some of the transformations are not written    in the form polynomial over polynomial`)     fi;    fi;   fi; fi; ans end:

 

The program  matrices  determines the matrix
symmetry corresponding to a given (list of) projective symmetries.  As discussed in the text, this only
requires determining an overall scalar multiple, which can be found by substituting the projective
symmetry into the form.  The output consists of each projective symmetry, the scalar factor $\mu $,
and the resulting matrix symmetry. 

>

matrices:=proc(form,n,L::list) local Q,ks,ksi,i,Sf,M; ksi:='ksi'; for i from 1 to nops(L) do  Sf:=simplify(denom(L[i])^n*form(L[i]));  ks:=quo(Sf,form(p),p);  ksi:=simplify(ks^(1/n),radical,symbolic);  M[i]:=matrix(2,2,[coeff(numer(L[i]),p)/ksi,  coeff(numer(L[i]),p,0)/ksi,coeff(denom(L[i]),p)/ksi,  coeff(denom(L[i]),p,0)/ksi]);  print(L[i],    mu=ksi,   map(simplify,M[i])); od; end:

 

The auxiliary function  l_f  uses polynomial division  to
reduce rational expressions to linear fractional form (when possible).  

>

l_f:=proc(x) local A,B,C,S,de,nu,r,R; global err;err:='err'; nu:=numer(x);   de:=denom(x); if type(nu,polynom(anything,p)) and     type(de,polynom(anything,p)) then  if degree(nu,p)+1=degree(de,p) then   A:=quo(de,nu,p,'B');   S:=1/A;R:=0  else   A:=quo(nu,de,p,'B');   if B=0 then S:=A;     R:=0;      else     C:=quo(de,B,p,'r');R:=simple(r);     S:=simplify(A+1/C)   fi;  fi;  if R=0 then       collect(S,p)  else    err:=1;x  fi; else  err:=2;x                                                   fi; end:

 

The auxiliary function simple helps to simplify rational
expressions by manipulating the numerator and denominator separately.
The simplified rational expression is returned.
 

>	simple:=proc(x) local nu,de,num,den; nu:=numer(x); de:=denom(x); num:=(simplify((nu,radical,symbolic))); den:=(simplify((de,radical,symbolic))); simplify(num/den); end:

 

Example: 

>	f:=p->p^3+1;

 

(1)

 

>	symm(f,3);

 

 

 

	(2)

 

>	matrices(f,3,%);

 

 

 

 

 

 

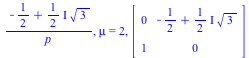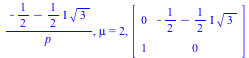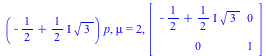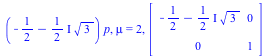	(3)

 

>	f:=p->p^2;

 

(4)

 

>	symm(f,3);

 

(5)

 

>	f:=p->p^4+2*I*sqrt(3)*p^2+1;

 

(6)

 

>	symm(f,4);

 

 

 

	(7)

 

>

 

>

 

>